About me and why I created this physics website.

Relative Velocity Problems
- Search Website
Real World Applications — for high school level and above
- Amusement Parks
- Battle & Weapons
- Engineering
- Miscellaneous
Education & Theory — for high school level and above
- Useful Formulas
- Physics Questions
- Example Mechanics Problems
- Learn Physics Compendium
Kids Section
- Physics For Kids
- Science Experiments
- Science Fair Ideas
- Science Quiz
- Science Toys
- Teacher Resources
- Commercial Disclosure
- Privacy Policy
© Copyright 2009-2024 real-world-physics-problems.com


- Exam Center
- Ticket Center
- Flash Cards
- Straight Line Motion
Relative Velocity Problems with Solutions: AP Physics 1
In this article, we solved some problems on relative velocities in one and two dimensions. We have chosen the problems in such a way that by solving them you can master this topic for the AP Physics 1 exam.
Relative Velocity Problems
Problem (1): A person walks across a raft at a speed of $0.5\,\rm m/s$ while his raft is traveling down the river at a speed of $1.8\,\rm m/s$ relative to the riverbank. Assuming that he walks perpendicular to the raft's motion relative to the river current, what is the person's velocity with respect to the river bank?
Solution : In this question, we are given the velocities in two directions, so it is a relative velocity problem in vector form. Let the river flows to the east and this direction is chosen as the positive $x$-direction. On the raft, the person walks due north and we choose this direction as the positive $y$-direction.
The safest method to analyze such problems is to draw a diagram and then apply the vector addition rules to obtain the desired quantity.
The river (water) flows at a speed of $1.8\,\rm m/s$ relative to the Ground (riverbank). We translate this phrase as $\vec{v}_{WG}$. On other hand, the velocity of the Person relative to the Raft is also designated as $\vec{v}_{PR}$.
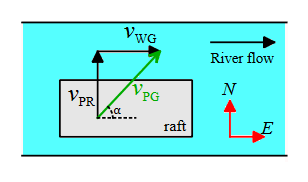
Tail-to-tip vector addition method: to add two vectors in this way, place the tail of the second vector on the tip of the first and connect the first tail to the tip of the second vector.
Here, the raft is moving in the direction of river flow to the right or $+x$-direction, i.e., $\vec{v}_{RG}=1.8(\hat{i}) \,\rm m/s$. On the other hand, the person is moving from one side to the other of the raft in the $+y$-direction, i.e., $\vec{v}_{PR}=0.5 (\hat{j}) \,\rm m/s $.
Therefore, the velocity vector of the person relative to the ground is written in the vector form as below \[\vec{v}_{PG}=0.5\,\hat{j}+1.8\,\hat{i}\] and its magnitude is also found using the Pythagorean theorem as follows \begin{align*} v_{PG}&=\sqrt{(1.8)^2+(0.5)^2} \\ &=1.87\,\rm m/s \end{align*} A you learned from vectors problems , the angle that this vector velocity is made with the positive $x$-axis is found using the following formula \begin{align*} \alpha &=\arctan\left(\frac{v_y}{v_x}\right) \\\\ &=\arctan\left(\frac{0.5}{1.8}\right) \\\\ &=15.5^\circ \end{align*} Therefore, from the point of view of an observer standing on the riverbank the person is walking across the raft at speed of about $1.8\,\rm m/s$.
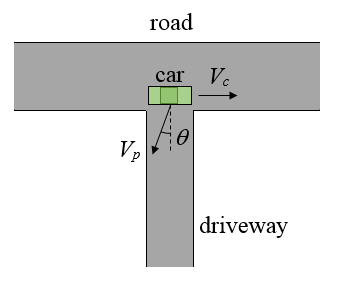
Problem (2): A flatcar is moving to the right at a speed of $13\,\rm m/s$ relative to a person standing on the ground. Someone is riding a bicycle on the flatcar with a speed of (a) $5\,\rm m/s$ to the right, (b) $5\,\rm m/s$ to the left relative to that person on the ground. What is the velocity (speed and direction) of the bicycle relative to the flatcar?
Solution : In this problem about relative velocities along a line, three velocities are given. Let the positive $x$-direction be to the right.
The velocity of the Flatcar relative to the Person, i.e., $\vec{v}_{FP}=13 (\hat{i}) \,\rm m/s$.
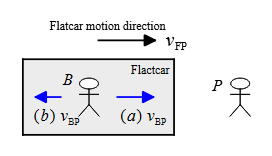
One of the easiest methods to solve such problems is to apply the inner subscript cancellation method. Here, the Bicycle's velocity relative to the Person, $\vec{v}_{BP}$ is asked. We know that the Bicycle is riding across the Flatcar, and the Flatcar also moves relative to the ground.
Thus, adding a $F$ subscript between $BP$ leads to the following partitioning for velocities \[\vec{v}_{BF}=\vec{v}_{BP}+\vec{v}_{PF}\] On the other hand, we know $\vec{v}_{PF}=-\vec{v}_{FP}$. Gathering these two relations and substituting the numerical values into it gives for part (a) \begin{align*} \vec{v}_{BF}&=\vec{v}_{BP}-\vec{v}_{FP} \\\\&=5-13\\\\&=-8\,\rm m/s \end{align*} The minus sign indicates that the bicycle is moving to the left ($-\hat{i}$) or in the opposite direction of the flatcar's motion.
Part (b) is left to you as a practice problem.
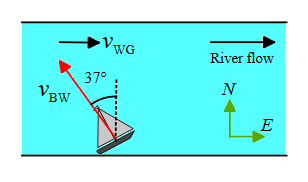
Problem (3): A boat with a speed of $10\,\rm m/s$ relative to the water leaves the south bank in the direction of $37^\circ$ west of north. The river is $300-\rm m$-wide and flows due east at a speed of $2\,\rm m/s$. What are the (a) magnitude and (b) direction of the boat's velocity relative to the ground? (c) How long does the boat take to reach the other side of the river?
Solution : This type of relative motion problem in two dimensions requires some information about resolving vectors into unit vectors along the $x$ and $y$ axes.
Sketching a vector diagram and applying the tip-to-tail vector sum rule to find the unknown velocity is not always the right method.
In this question, we see that the two velocities are not perpendicular to each other, so the triangle that is made is not a right triangle and correspondingly, we cannot use the Pythagorean theorem or angle formula to find its magnitude and direction.
When the given velocities were perpendicular to each there, then we could use the following well-known vector addition equation \[\vec{v}_{BG}=\vec{v}_{BW}+\vec{v}_{WG}\]
Finally, a lengthy question is over.
Problem (4): Ali, driving north at speed of $50\,\rm mph$, and Sara, driving east at $45\,\rm mph$, are approaching an intersection. What is Ali's speed as seen by Sara?
Solution : This problem involves two velocities in two dimensions, so it is a relative velocity question using vectors. Thus, it is better to establish a coordinate system in which the $x$ and $y$ axes correspond to the east and north directions.
Ali and Sara are driving relative to the Ground at speeds of $\vec{v}_{AG}=50(\hat{j}) \,\rm mph$ and $\vec{v}_{SG}=45(\hat{i}) \,\rm mph$. In all relative velocity problems, there are always two reference frames. In this case, the ground is the one and the other can be Ali or Sara.
Ali's velocity relative to Sara, i.e., $v_{AS}$ is unknown and needs to be determined. We only have Ali's and Sara's speeds relative to the ground, $v_{Ag}$ and $v_{Sg}$. To write the correct vector addition $v_{AS}$, we apply the inner subscript cancellation method by inserting ground (G) between Ali (A) and Sara (S) subscripts as follows \[\vec{v}_{AS}=\vec{v}_{AG}+\vec{v}_{GS}\] Now if look at this relation carefully, you notice that in the problem the velocity of Sara relative to the ground, $v_{SG}$ was given. $v_{GS}$ means the Ground's velocity relative to Sara. If Sara moves toward the right relative to the ground, the ground also moves to the left as seen by Sara.
Keep in mind, as a rule, that in all relative velocities we have the following important note about two reference frames moving relative to each other \[\vec{v}_{AB}=-\vec{v}_{BA}\] Applying this fact to the above vector sum, we have \begin{align*} \vec{v}_{AS}&=\vec{v}_{AG}+\vec{v}_{GS} \\\\ &=\vec{v}_{AG}-\vec{v}_{SG} \\\\ &= 50\hat{j}-45\hat{i} \end{align*} Given this vector, applying the Pythagorean theorem gives us his magnitude (Ali's speed) \[v_{AS}=\sqrt{50^2+(-45)^2}=67.2\,\rm mph\] And his direction as seen by Sara is found using the following formula measured counterclockwise from the $+x$-direction. \begin{align*} \alpha&=\arctan\left(\frac{v_y}{v_x}\right) \\\\ &=\arctan\left(\frac{50}{-45}\right) \\\\ &=-48.0^\circ \end{align*} There is a subtlety about using this formula to find the direction. If a vector is in the second or third quadrant, then add $180^\circ$ to the angle obtained by the above formula to find the correct angle. Here, $\vec{v}_{AS}$ is in the second quadrant. Thus, we have \[\beta=180^\circ-48^\circ=\boxed{132^\circ}\]
Problem (5): Two cars are approaching at right angles to a corner. Car $1$ moves due east at a speed of $v_{1g}=45\,\rm m/s$ with respect to the ground and car $2$ due north at $v_{2g}=35\,\rm m/s$. (a) What is the relative velocity of car $1$ as seen by car $2$? (b) What is the relative velocity of car $2$ as seen by car $1$?
Solution : Assign a coordinate system in which the east and north directions correspond to the $x$ and $y$ axes. We simplify our known as below: $\vec{v}_{1g}=45(\hat{i}) \,\rm m/s$ and $\vec{v}_{2g}=35(\hat{j}) \,\rm m/s$.
(a) We label the velocity of car $1$ relative to car $2$ by $\vec{v}_{12}$, add ground g as an inner subscript between $12$, and write the vector addition equation as below \begin{align*} \vec{v}_{12}&=\vec{v}_{1g}+\vec{v}_{g2} \\\\ &=\vec{v}_{1g}-\vec{v}_{2g} \\\\ &= 45\hat{i}-35\hat{j} \end{align*} This velocity vector lies in the fourth quadrant whose magnitude with the positive $x$ direction is found as \begin{align*} \alpha&=\arctan\left(\frac{v_y}{v_x}\right) \\\\ &=\arctan\left(\frac{-35}{45}\right) \\\\ &=\boxed{-38^\circ} \end{align*} The negative indicates an angle below the horizontal. The Pythagorean theorem gives its magnitude (speed) \[v_{12}=\sqrt{45^2+(-35)^2}=57\,\rm m/s\] In summary, from the point of view of car $2$, car $1$ moves with a speed of $57\,\rm m/s$ at $38^\circ$ angle below horizontal or $38^\circ$ south of east.
(b) Similar to the previous part, solve this section.
\item Problem (6): A boat is traveling due north at $6\,\rm m/s$ while a cruise ship heads $45^\circ$ north of east at $4\,\rm m/s$. What are the $x$ and $y$ components of the velocity of the boat relative to the cruise ship?
Solution : Take the north and east as positive $y$ and $x$ directions. North of east means you first stand facing east then turn leftward. The cruise ship's velocity vector lies in the first quadrant with the following components \[\vec{v}_{CG}=4(\cos 45^\circ\hat{i}+\sin 45^\circ\hat{j})\] The Boat's velocity relative to the Ground is also given as $\vec{v}_{BG}=6(\hat{j}) \,\rm m/s$. Now to find the cruise's velocity relative to the boat, we can either draw a vector diagram and use it to write the correct form of vector addition or use the inner subscript cancellation method.
Since the two velocities are not perpendicular to each other, the vector diagram isn't a helpful method.
We are asked $v_{BC}$. The inner subscript cancellation method tells us to add the Ground G between the $BC$ subscripts (since we are given only $v_{BG}$ and $v_{CG}$) as below \[\vec{v}_{BC}=\vec{v}_{BG}+\vec{v}_{GC}\] Now using the fact that $\vec{v}_{GC}=-\vec{v}_{CG}$, we have \begin{align*} \vec{v}_{BC}&=\vec{v}_{BG}-\vec{v}_{CG} \\\\ &=6\hat{j}-4(\cos 45^\circ\hat{i}+\sin 45^\circ\hat{j}) \\\\ &=-2\sqrt{2} \hat{i}+(6-2\sqrt{2}) \hat{j} \end{align*} The Pythagorean theorem gives us its magnitude or the speed of Boat relative to the cruise ship. \begin{align*} v_{CG}&=\sqrt{\left(-2\sqrt{2}\right)^2+\left(6-2\sqrt{2}\right)^2} \\\\ &=4.2\,\rm m/s\end{align*} Hint, take $\sqrt{2}=1.4$ and use a calculator to solve this relation. Finally, its direction measured counterclockwise from the positive $x$-axis is \begin{align*} \alpha&=\arctan\left(\frac{v_y}{v_x}\right) \\\\ &=\arctan\left(\frac{6-2\sqrt{2}}{-2\sqrt{2}}\right) \\\\ &=-66^\circ \end{align*} Again, $\vec{v}_{BC}$ is in the second quadrant, so the true angle is \[\beta=180^\circ+(-66^\circ)=\boxed{114^\circ}\]
Problem (7): A person in a basket of a hot-air balloon throws a ball horizontally into the air with a speed of $6\,\rm m/s$. As seen by an observer standing on the ground, what initial velocity does the ball have if, the balloon is (a) rising at $2\,\rm m/s$ relative to the ground, (b) descending at $2\,\rm m/s$ relative to the ground?
Solution : We are given the ball's velocity relative to the Balloon, say to the right horizontally, i.e., $\vec{v}_{bB}=6(\hat{i}) \,\rm m/s$. For this problem, we adopt a coordinate system in which up and right correspond to the $\hat{j}$ and $\hat{i}$, respectively.
(a) In this part, the Balloon's velocity (magnitude and direction) with respect to the ground is given, i.e., $\vec{v}_{BG}=2(\hat{j}) \,\rm m/s$. The best and easiest method to solve every relative motion question in two dimensions is using the $\hat{i}$ and $\hat{j}$ approach.
The unknown is the ball's velocity relative to the ground, i.e., $\vec{v}_{bG}$. We can simply combine these velocities using the cancellation of inner subscripts method as follows \begin{align*} \vec{v}_{bG}&=\vec{v}_{bB}+\vec{v}_{BG} \\\\ &=6\hat{i}+2\hat{j} \end{align*} Pay attention that the ball moves relative to the Balloon and the Balloon is also moves relative to the Ground, so we can add Balloon as a middle subscript between $v_{bG}$ and break it into two parts as $v_{bB}$ and $v_{BG}$. Given the velocity vector $\vec{v}_{bB}$, one can find its magnitude \[v_{bB}=\sqrt{6^2+2^2}=6.3\,\rm m/s\] and its direction as measured counterclockwise from $+x$-direction \begin{align*} \alpha&=\arctan\left(\frac{y-component}{x-component}\right) \\\\ &=\arctan\left(\frac{2}{6}\right) \\\\ &=18.5^\circ \end{align*} Therefore, from the point of view of an observer standing on the ground, he/she sees that the ball is thrown with an initial speed of $6.3\,\rm m/s$ at an angle of about $18^\circ$ above the horizontal.
(b) In this case, the Balloon is descending at $2\,\rm m/s$ relative to the Ground, i.e., $\vec{v}_{BG}=2(-\hat{j}) \,\rm m/s$. Similar to the previous part, the ball's velocity relative to the Ground is written in vector addition form as below \begin{align*} \vec{v}_{bG}&=\vec{v}_{bB}+\vec{v}_{BG} \\\\ &=6\,\hat{i}+2(-\hat{j}) \end{align*} Given this, its magnitude and direction are found as below \begin{align*} v_{bB}&=\sqrt{6^2+(-2)^2}=6.3\,\rm m/s\end{align*} and \begin{align*} \alpha&=\arctan\left(\frac{v_y}{v_x}\right) \\\\ &=\arctan\left(\frac{-2}{6}\right) \\\\ &=-18.5^\circ \end{align*} Thus, the observer standing on the ground, sees the ball is thrown away from the balloon at about $18^\circ$ below the horizontal with the same speed as before.
Problem (8): An aircraft is flying in a crosswind due north while its speed indicator shows $350\,\rm km/h$ relative to the air. The wind also blows from west to east at a constant speed of $50\,\rm km/h$ relative to the ground. What is the direction and speed of the aircraft relative to the ground?
Solution : First of all, draw a vector diagram and illustrate all the given velocities on it then apply the tip-to-tail vector sum rule to write the correct form of the combined velocities.
In this question, it's said explicitly that the two velocities make a right angle with each other, one is moving to the north and the other to the east.
The given information is the plane's speed relative to the air, i.e., $v_{PA}=350\,\rm km/h$, and the Air's speed with respect to the Ground, i.e., $v_{AG}=50\,\rm km/h$.
The vector diagram above illustrates that the correct form of vector addition reads \[\vec{v}_{PG}=\vec{v}_{PA}+\vec{v}_{AG}\] Applying the Pythagorean theorem gives us the plane's velocity relative to the ground \begin{align*} v_{PG}&=\sqrt{(350)^2+(50)^2} \\\\ &=354\,\rm km/h \end{align*} The vector addition, in this case, form a right triangle so we don't need the velocity components to find the direction (a long way). In such cases, according to the figure of the right triangle, we use the definition of one of the trigonometry functions.
The direction of the plane, as seen from the point of view of an observer standing on the ground, is found by applying the definition of the tangent function and then taking its inverse as below \begin{align*} \alpha&=\arctan\left(\frac{50}{350}\right) \\\\ &=8^\circ \end{align*}
Problem (9): A $500-\rm m$-wide river flows due south at a constant speed of $3\,\rm m/s$. A man in a motorboat travels across the river due east at $5\,\rm m/s$. (a) What is the velocity (magnitude and direction) of the boat relative to the earth (ground)? (b) How much time is required for the man to cross the river? (c) Starting from the south bank, how far will he reach the opposite bank?
Solution : Again, sketch a vector diagram and indicate all the velocity vectors on it. Take east as the positive $x$-direction, and north as the positive $y$-direction.
The river flows southward or the negative $y$-direction relative to the ground (or an observer standing on the riverbank), so it has no $x$ component, i.e., $\vec{v}_{RG}=3\,\rm m/s\, (-\hat{j})$.
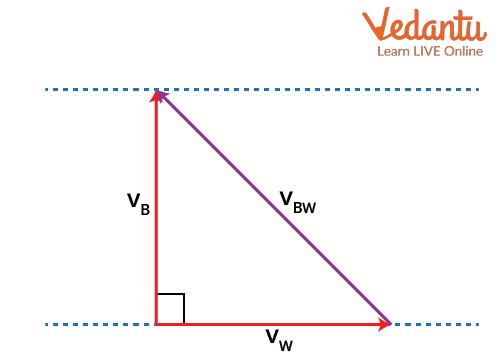
On the other hand, the boat travels eastward or the positive $x$-direction relative to the river flow (water), i.e., $\vec{v}_{BW}=5\,\rm m/, \, (\hat{i})$.
(a) The boat's velocity with respect to the ground, $\vec{v}_{BG}$, is the vector sum of its velocity relative to the water, $\vec{v}_{BW}$, plus the velocity of the water with respect to the ground (river bank), $\vec{v}_{WG}$ \begin{align*} \vec{v}_{BG}&=\vec{v}_{BW}+\vec{v}_{WG} \\\\ &=5\,\hat{i}+3\,(-\hat{j}) \end{align*} (a) As indicated in the vector diagram above, $\vec{v}_{BW}$ is perpendicular to $\vec{v}_{WG}$, so applying the Pythagorean theorem gives us $v_{BG}$ \begin{align*} v_{BG}&=\sqrt{v_{BW}^2+v_{WG}^2} \\\\ &=\sqrt{5^2+(-3)^2} \\\\ &=5.8\,\rm m/s \end{align*} To find the direction either we can use the figure and the definition of the $sin$ function or use the standard formula once the components are given.
From the figure, we have \[\sin\theta=\frac{v_{WG}}{v_{BG}}=\frac{3}{5.8}\] Taking the inverse sine, $\arcsin$ or $\sin^{-1}$, from both sides, gives \[\theta=\sin^{-1}\left(\frac{3}{5.8}\right)=31.1^\circ\] (b) The time required for the man (or motorboat) to cross the river is obtained using the definition of average velocity, $v=\frac{D}{t}$. Given the river's width $D=500\,\rm m$, and the corresponding velocity in this direction $v_{BW}$, we have \[t=\frac{D}{v_{BW}}=\frac{500}{5}=100\,\rm s\] Thus, it takes $100\,\rm s$ or about $1.7$ minutes for the man to travel the width of the river.
(c) During the time the boat crosses the river's width, the water stream with a speed of $v_{WG}$ will displace the boat downstream, a distance of \[ d=v_{WG}t=3\times 100=300\,\rm m\]
When object A moves relative to object B with velocity $\vec{v}_{AB}$, and B also travels relative to object C (or an observer) with $\vec{v}_{BC}$, then the velocity of object A with respect to object C, designated by $\vec{v}_{AC}$, is determined by the following vector addition equation \[\vec{v}_{AC}=\vec{v}_{AB}+\vec{v}_{BC}\]
Author : Dr. Ali Nemati Published : Feb 2, 2023
© 2015 All rights reserved. by Physexams.com
Riverboat Problems
Kinematics Exams and Solutions

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

11A: Relative Velocity
- Last updated
- Save as PDF
- Page ID 2467

- Jeffrey W. Schnick
- Saint Anselm College
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Vectors add like vectors, not like numbers. Except in that very special case in which the vectors you are adding lie along one and the same line, you can’t just add the magnitudes of the vectors.
Imagine that you have a dart gun with a muzzle velocity of \(45 mph\). Further imagine that you are on a bus traveling along a straight highway at \(55 mph\) and that you point the gun so that the barrel is level and pointing directly forward, toward the front of the bus. Assuming no recoil, as it leaves the muzzle of the gun, how fast is the dart traveling relative to the road? That’s right! \(100 mph\). The dart is already traveling forward at \(55 mph\) relative to the road just because it is on a bus that is moving at \(55 mph\) relative to the road. Add to that the velocity of \(45 mph\) that it acquires as a result of the firing of the gun and you get the total velocity of the dart relative to the road. This problem is an example of a class of vector addition problems that come under the heading of “Relative Velocity.” It is a particularly easy vector addition problem because both velocity vectors are in the same direction. The only challenge is the vector addition diagram, since the resultant is right on top of the other two. We displace it to one side a little bit in the diagram below so that you can see all the vectors. Defining
\(\vec{V}_{BR}\) to be the velocity of the bus relative to the road, \(\vec{V}_{DB}\) to be the velocity of the dart relative to the bus, and \(\vec{V}_{DR}\) to be the velocity of the dart relative to the road; we have The vector addition problem this illustrates is \[\vec{V}_{DR}=\vec{V}_{BR}+\vec{V}_{DB} \nonumber \] If we define the forward direction to be the positive direction, then, because the vectors we are adding are both in the same direction, we are indeed dealing with that very special case in which the magnitude of the resultant is just the sum of the magnitudes of the vectors we are adding: \[\vec{V}_{DR}=\vec{V}_{BR}+\vec{V}_{DB} \nonumber \] \[V_{DR}=V_{BR}+V_{DB} \nonumber \] \[V_{DR}=55mph+45mph \nonumber \] \[V_{DR}=100mph \nonumber \] \(\vec{V}_{DR}=100mph\) in the direction in which the bus is traveling
You already know all the concepts you need to know to solve relative velocity problems (you know what velocity is and you know how to do vector addition) so the best we can do here is to provide you with some more worked examples. We’ve just addressed the easiest kind of relative velocity problem, the kind in which all the velocities are in one and the same direction. The second easiest kind is the kind in which the two velocities to be added are in opposite directions.
A bus is traveling along a straight highway at a constant \(55 mph\). A person sitting at rest on the bus fires a dart gun that has a muzzle velocity of \(45 mph\) straight backward, (toward the back of the bus). Find the velocity of the dart, relative to the road, as it leaves the gun. Again defining: \(\vec{V}_{BR}\) to be the velocity of the bus relative to the road, \(\vec{V}_{DB}\) to be the velocity of the dart relative to the bus, and \(\vec{V}_{DR}\) to be the velocity of the dart relative to the road, and defining the forward direction to be the positive direction; we have \[\vec{V}_{DR}=\vec{V}_{BR}+\vec{V}_{DB} \nonumber \] \[V_{DR}=V_{BR}-|V_{DB}| \nonumber \] \[V_{DR}=55mph-45mph \nonumber \] \[V_{DR}=10mph \nonumber \] \(\vec{V}_{DR}=10mph\) in the direction in which the bus is traveling It would be odd looking at that dart from the side of the road. Relative to you it would still be moving in the direction that the bus is traveling, tail first, at \(10 mph\). The next easiest kind of vector addition problem is the kind in which the vectors to be added are at right angles to each other. Let’s consider a relative velocity problem involving that kind of vector addition problem.
A boy sitting in a car that is traveling due north at \(65 mph\) aims a bb gun (a gun which uses a compressed gas to fire a small metal or plastic ball called a bb), with a muzzle velocity of \(185 mph\), due east, and pulls the trigger. recoil (the backward movement of the gun resulting from the firing of the gun) is negligible. in what compass direction does the bb go defining \(\vec{v}_{cr}\) to be the velocity of the car relative to the road, \(\vec{v}_{bc}\) to be the velocity of the bb relative to the car, and \(\vec{v}_{br}\) to be the velocity of the bb relative to the road; we have \[tan\theta=\dfrac{v_{bc}}{v_{cr}} \nonumber \] \[\theta=tan^{-1}\dfrac{v_{bc}}{v_{cr}} \nonumber \] \[\theta=tan^{-1}\dfrac{185 mph}{65 mph} \nonumber \] \[\theta=70.6^\circ \nonumber \] the bb travels in the direction for which the compass heading is \(70.6^\circ\)., a boat is traveling across a river that flows due east at \(8.50 m/s\). the compass heading of the boat is \(15.0^\circ\). relative to the water, the boat is traveling straight forward (in the direction in which the boat is pointing) at \(11.2 m/s\). how fast and which way is the boat moving relative to the banks of the river okay, here we have a situation in which the boat is being carried downstream by the movement of the water at the same time that it is moving relative to the water. note the given information means that if the water was dead still, the boat would be going 11.2 m/s at \(15.0^\circ\) east of north. the water, however, is not still. defining \(\vec{v}_{wg}\) to be the velocity of the water relative to the ground, \(\vec{v}_{bw}\) to be the velocity of the boat relative to the water, and \(\vec{v}_{bg}\) to be the velocity of the boat relative to the ground; we have solving this problem is just a matter of following the vector addition recipe. first we define \(+x\) to be eastward and \(+y\) to be northward. then we draw the vector addition diagram for \(\vec{v}_{wg}\). breaking it up into components is trivial since it lies along the x-axis: breaking \(\vec{v}_{bw}\) does involve a little bit of work: now we add the \(x\) components to get the \(x\)-component of the resultant \[v_{bgx}=v_{wgx}+v_{bwx} \nonumber \] \[v_{bgx}=8.50\dfrac{m}{s}+2.899\dfrac{m}{s} \nonumber \] \[v_{bgx}=11.299\dfrac{m}{s} \nonumber \] and we add the y components to get the y-component of the resultant: \[v_{bgy}=v_{wgy}+v_{bwy} \nonumber \] \[v_{bgy}=0\dfrac{m}{s}+10.82\dfrac{m}{s} \nonumber \] \[v_{bgy}=10.82\dfrac{m}{s} \nonumber \] now we have both components of the velocity of the boat relative to the ground. we need to draw the vector component diagram for \(\vec{v}_{bg}\) to determine the direction and magnitude of the velocity of the boat relative to the ground. we then use the pythagorean theorem to get the magnitude of the velocity of the boat relative to the ground, \[\vec{v}_{bg}=\sqrt{v_{bgx}^2+v_{bgy}^2} \nonumber \] \[\vec{v}_{bg}=\sqrt{(11.299m/s)^2+(10.82m/s)^2} \nonumber \] \[\vec{v}_{bg}=15.64m/s \nonumber \] and the definition of the tangent to determine the direction of \(\vec{v}_{bg}\): \[tan\theta=\dfrac{v_{bgy}}{v_{bgx}} \nonumber \] \[\theta=tan^{-1}\dfrac{v_{bgy}}{v_{bgx}} \nonumber \] \[\theta=tan^{-1}\dfrac{10.82m/s}{11.299m/s} \nonumber \] \[\theta=43.8^\circ \nonumber \] hence, \(\vec{v}_{bg}=15.64m/s\) at \(43.8^\circ\) north of east..
- Introduction To Motion
- Relative Velocity
Relative velocity in two dimensions
Relative velocity:.
We encounter occasions where one or more objects move in a frame which is non-stationary with respect to another observer. For example, a boat crossing a river that is flowing at some rate or an aeroplane encountering wind during its motion. In all such instances, to describe the object’s complete motion, we need to consider the effect that the medium is causing on the object. While doing so, we calculate the relative velocity of the object considering the velocity of the particle as well as the velocity of the medium. Here, we will learn how to calculate the relative velocity .
What is Relative Velocity?
Let us consider two objects, A and B moving with velocities V a and V b with respect to a common stationary frame of reference , say the ground, a bridge or a fixed platform.
The velocity of the object A relative to the object B can be given as,
\(\begin{array}{l}V_{ab}=V_{a}-V_{b}\end{array} \)
Similarly, the velocity of the object B relative to that of object a is given by,
\(\begin{array}{l}V_{ba}=V_{b}-V_{a}\end{array} \)
From the above two expressions, we can see that
\(\begin{array}{l}V_{ab}=-V_{ba}\end{array} \)
Although the magnitude of both the relative velocities is equal to each other. Mathematically,
\(\begin{array}{l}\left |V_{ab} \right |=\left |V_{ba} \right |\end{array} \)
Examples of Relative Velocity
We can understand the concept of relative velocity more clearly with the help of the following example.
Example : A plane is travelling at velocity 100 km/hr, in the southward direction. It encounters wind travelling in the west direction at a rate of 25 km/hr. Calculate the resultant velocity of the plane.
Given, the velocity of the wind = V w = 25 km/hr
The velocity of the plane = V a = 100 km/hr
The relative velocity of the plane with respect to the ground can be given as
The angle between the velocity of the wind and that of the plane is 90°. Using the Pythagorean theorem, the resultant velocity can be calculated as,
R 2 = (100 km/hr) 2 + (25 km/hr) 2
R 2 = 10 000 km 2 /hr 2 + 625 km 2 /hr 2
R 2 = 10 625 km 2 /hr 2
Hence, R = 103.077 km/hr
Using trigonometry, the angle made by the resultant velocity with respect to the horizontal plane can be given as,
\(\begin{array}{l}tan\theta =(\frac{wind \: velocity}{aiprplane\: velocity})\\ \\ tan\theta =(\frac{25}{100})\\ \\ \theta =tan^{-1}\frac{1}{4}\\ \\ \theta =14.0^{\circ}\end{array} \)
Relative Velocity Problems
1) What is relative velocity?
Relative velocity is defined as the velocity of an object B in the rest frame of another object A.
2) A motorcycle travelling on the highway at a velocity of 120 km/h passes a car travelling at a velocity of 90 km/h. From the point of view of a passenger on the car, what is the velocity of the motorcycle?
Let us represent the velocity of the motorcycle as V A and the velocity of the car as V B .
Now, the velocity of the motorcycle relative to the point of view of a passenger is given as
V AB = V A – V B
Substituting the values in the above equation, we get
V AB = 120 km/h – 90 km/h = 30 km/h
Hence, the velocity of the motorcycle relative to the passenger of the car is 30 km/h.
3) A swimmer swimming across a river flowing at a velocity of 4 m/s swims at the velocity of 2 m/s. Calculate the actual velocity of the swimmer and the angle.
The actual velocity of the swimmer can be found out as follows:
The angle is calculated as follows:
4) A person in an enclosed train car, moving at a constant velocity, throws a ball straight up into the air in her reference frame.
- At what point, does the ball land?
- Where does the ball land if the car slows down?
- Where does the ball land if the car speeds up?
- Where does it land if the car rounds a turn?
- The ball lands at the point from which it was thrown, i.e. back to the thrower’s hand.
- It lands in front of the point from which it was thrown.
- It lands behind the point from which it was thrown.
- The ball will land to the left of the point from which it was thrown if the car takes a right turn and vice versa.
5) An aeroplane A flies with a velocity of 450 m/s to the north, while an aeroplane B travels at a velocity of 500 m/s to the south beside aeroplane A. Calculate the relative velocity of the aeroplane A with respect to aeroplane B. Solution:
The relative velocity of aeroplane A with respect to the velocity of aeroplane B is calculated as follows:
Substituting the values in the equation, we get
V AB = 450 m/s – (–500 m/s) = 950 m/s
The velocity of aeroplane B is considered negative, as it flies in the opposite direction to the of aeroplane A.
Stay tuned with BYJU’S to learn more about the concept of relative velocity, relative motion and other related topics.

Frequently Asked Questions – FAQs
What is relative velocity, a motorcycle travelling on the highway at a velocity of 120 km/h passes a car travelling at a velocity of 90 km/h. from the point of view of a passenger in the car, what is the velocity of the motorcycle.
Now, the velocity of the motorcycle relative to the point of view of a passenger is given as, V AB = V A – V B
Substituting the values in the above equation, we get V AB = 120 km/h – 90 km/h = 30 km/h
State if the statement is true or false: Relative velocity can be negative.
The above statement is true. Relative velocity can be negative. As relative velocity is the difference between two velocities irrespective of their magnitude, it can be negative.
What is the difference between velocity and relative velocity?
The difference between velocity and relative velocity is that velocity is measured with respect to a reference point which is relative to a different point. While relative velocity is measured in a frame where an object is either at rest or moving with respect to the absolute frame.
What is the need of using relative velocity?
The need for using relative velocity is that it is used for differentiating if the object is at rest or moving.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
Request OTP on Voice Call
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Post My Comment
Two bodies A and B are moving in the same direction with velocities VA and VB , where VA>VB and they start symultaneously from different points, and B is in front of A. Represent their relative motion in a position time graph. Explain their relative velocity during the motion
- Share Share
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.

Description This is a simulation of a boat crossing a river. Adjust the direction the boat is aimed, the boat's velocity relative to the river, and the river's velocity relative to the earth. Press the "Run" button to watch the boat's trip across the river. Questions to answer: 1) What direction should the boat be aimed to get to the other side of the river in the least amount of time? 2) What direction does the boat need to be aimed to get to the point directly across the river? 3) If the boat is aimed directly across the river, does the speed of the river's current affect the amount of time it takes the boat to cross the river?
Talk to our experts
1800-120-456-456
River Boat Problem in 2D From Relative Velocity - JEE Important Topic
- River Boat Problem Relative Velocity In 2d

A Brief Introduction to Relative Velocity
We come into situations when one or more objects move in a non-stationary frame with respect to another observer. For example: a boat crossing a fast-flowing river or an aeroplane flying in the air encountering wind. In all these cases, we must consider the medium's effect on the item to characterise the object's whole motion. We calculate the relative velocity of the object while doing so, taking into account the particle's velocity as well as the velocity of the medium. Since velocity is a vector, the calculations of relative velocity include vector algebra. We’ll look at the problem of relative velocity in more detail throughout this article and discuss river velocity, river boat problems and solutions to relative velocity.
Examples and Mathematical Formulation of Relative Velocity
We all have encountered relative velocity at some point. Some classic examples of relative velocity include situations where, while travelling by automobile, bus or train, you may see that the trees, buildings and other objects outside are moving backwards. Is it true, however, that they are going backwards? No! You're completely aware that your vehicle is moving while the trees remain motionless on the ground. But, if that's the case, why are the trees travelling backwards? Also, even though they are moving, your fellow passengers appear to be motionless to you.
This is where the concept of relative velocity comes into play. The passengers appear motionless to you because they are at rest, relative to you. However, to someone on the ground who isn’t moving, your fellow passengers are in motion, relative to them. You are also in motion relative to someone on the ground. Although the person on the ground might not be moving, according to you they are moving backwards and they have a velocity relative to you.
Let’s consider two objects and name them objects A and B. Suppose object A has velocity v A and object B has velocity v B and they are moving relative to some common stationary frame of reference. This frame of reference could be anything; the ground, a lamppost, a bridge, etc.
Relative velocity is just the difference between the velocities of the objects. Already emphasised before, this difference is not the ordinary difference because velocities are vectors. So, they will follow the rules of vector algebra.
The velocity of object A relative to B is represented as v AB . The formula for this is:
$v_{A B}=v_{A}-v_{B}$
Similarly, the velocity of object B relative to A is represented by v BA and its formula is:
$v_{B A}=v_{B}-v_{A}$
From the expressions of v AB and v BA , we can say that they both are additive inverses of each other. This means that:
$v_{A B}=-v_{B A}$
This means that v AB has a direction that is opposite to v BA . Even though they have opposite directions, their magnitude remains the same.
$\left|v_{A B}\right|=\left|v_{B A}\right|$
River Boat Problem in 2D
When a boat is moving through a river, it is affected by the velocity of the water. The directions of the velocities of the boat and the river are usually different. The motion of the boat is influenced by the relative velocity between them. As usual, the concept of relative velocity will be applied and then the problems will be solved accordingly.
If a motorboat was heading straight across a river, it would not reach the point exactly opposite to where it started from. This is due to the river current that influences its motion.
Let’s suppose that we have a motorboat which is moving with a velocity of 6 $\dfrac{m}{s}$ directly across the river. If the river has a velocity downstream, the actual resultant velocity of the motorboat will not be the same as it was initially. The velocity of the boat will be a bit more than 6 $\dfrac{m}{s}$ and it will not be in the direction straight across the river, but at some direction downstream with a certain angle.
The shortest path in the river boat problems is when the boat moves perpendicular to the river current. This whole situation will become clear with some numerical examples that we’ll see in the next section.
To solve any river boat problem, two things are to be kept in mind.
A boat's speed with respect to the water is the same as its speed in still water.
The velocity of the boat relative to water is equal to the difference in the velocities of the boat relative to the ground and the velocity of the water with respect to the ground. If v BW is the velocity of the boat with respect to the water, and v B , v W are the velocities of the boat and water with respect to the ground respectively, then:
$v_{B W}=v_{B}-v_{W}$
Boat and River Current Velocities
Crossing The River in The Shortest Time
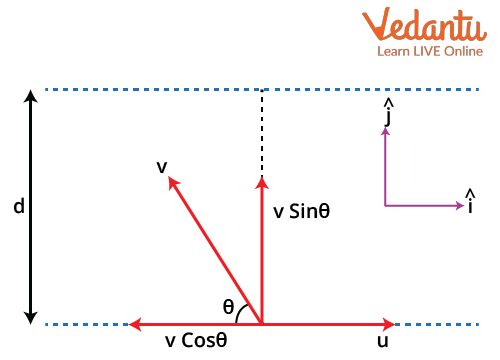
Schematic Diagram of a Boat Going Across a River
Suppose that u is the velocity of the river and v is the velocity of the boat. The boat moves at some angle $\theta$ with respect to the horizontal as shown in the figure. The total velocity of the boat will be the sum of the velocity of the boat with respect to the ground and the velocity of the river. This will be given as
$\begin{align} &v_{b}=\vec{v}+\vec{u} \\ \\ &v_{b}=-v \cos \theta \hat{i}+v \sin \theta \hat{j}+u \hat{i} \\ \\ &v_{b}=(-v \cos \theta+u) \hat{i}+v \sin \theta \hat{j} \end{align}$
The boat needs to move in the vertical direction in order to make it across the river so only the vertical component of the velocity will be used in getting it across the river. The vertical component is $v\sin{\theta}$. The width of the river is d and so the time taken to cross the river will be
$t=\dfrac{d}{v\sin{\theta}}$
For a minimum time
$\sin{\theta}=1$
$\theta=90^{\circ}$
This means that the minimum time to cross the river will be
$t_{min}=\dfrac{d}{v}$
Crossing the River Along the Shortest Path
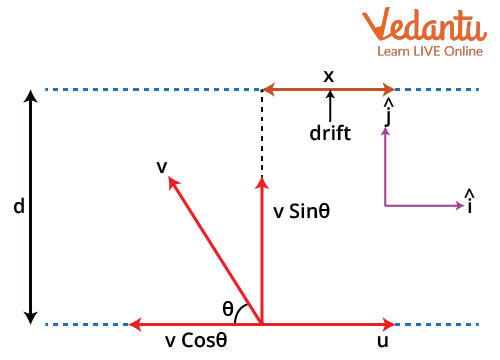
Schematic Diagram of A Boat Going Across The River With Some Drift
For the boat to go across the river along the shortest path, the drift x should be minimum or more precisely zero. The drift x will be zero when the velocity in the i direction will be zero. This means that
$\begin{align} &u-v \cos \theta=0 \\ \\ &v \cos \theta=u \\ \\ &\cos \theta=\dfrac{u}{v} \\ \\ &\theta=\cos ^{-1}\left(\dfrac{u}{v}\right) \end{align}$
So in order for the boat to go along the shortest path it has to go at an angle of $\theta=\cos^{-1}\left(\dfrac{u}{v}\right)$ with the vertical.
The time for the shortest path will be given as
Now we have $\cos{\theta}=\dfrac{u}{v}$ and we know that
$\begin{align} &\sin ^{2} \theta+\cos ^{2} \theta=1 \\ \\ &\sin ^{2} \theta=1-\cos ^{2} \theta \\ \\ &\sin \theta=\sqrt{1-\cos ^{2} \theta} \end{align}$
Putting the value of $\sin{\theta}$ will give
$\begin{align} &\sin \theta=\sqrt{1-\left(\dfrac{u}{v}\right)^{2}} \\ \\ &\sin \theta=\sqrt{1-\dfrac{u^{2}}{v^{2}}} \\ \\ &\sin \theta=\sqrt{\dfrac{v^{2}-u^{2}}{v^{2}}} \\ \\ &\sin \theta=\dfrac{\sqrt{v^{2}-u^{2}}}{v} \end{align}$
Inserting this in the expression for time gives
$\begin{align} &t=\dfrac{d}{v\left(\dfrac{\sqrt{v^{2}-u^{2}}}{v}\right)} \\ &t=\dfrac{ d}{\sqrt{v^{2}-u^{2}}} \end{align}$
This is the time taken along the shortest path.
Numerical Examples of Relative Velocity River Boat Problems
Example 1: A boat has a velocity of 10$\dfrac{km}{hr}$ in still water and it crosses a river of width 2 km. If the boat crosses the river along the shortest path possible in 30 minutes, calculate the velocity of the river water.
Solution:
Since it is given that the boat crosses the river in the shortest path possible, it means that the boat moves perpendicular to the river current.
Now, we have:
v BW = 10 $\dfrac{km}{hr}$, v w =? .
The distance d=2 km.
Time taken is, t=20 min= 0.5 hr.
We know that the velocity of the boat in respect to water is:
Since the boat is moving perpendicular to the water, we can apply Pythagoras theorem to find the magnitude of the resultant velocity of the boat.
This means:
$\left|v_{B W}\right|^{2}=\left|v_{B}\right|^{2}+\left|v_{W}\right|^{2}$....(1)
Velocities of Boat and the Water
We have been given that the boat covers a distance of 2km in 0.5 hr.
This means that the velocity of the boat with respect to the ground will be:
$\begin{align} &v_{B}=\dfrac{2}{0.5} \\ &v_{B}=4 \dfrac{\mathrm{~km}}{ \mathrm{hr}} \end{align}$
Substituting the values in equation (1) we get,
$\begin{align} &10^{2}=4^{2}+\left|v_{W}\right|^{2} \\ \\ &100-16=\left|v_{W}\right|^{2} \\ \\ &\sqrt{84}=v_{W} \\ \\ &9.16 \simeq v_{W} \end{align}$
So, the velocity of the river water is approximately 9.16 $\dfrac{km}{hr}$.
Example 2: The velocity of a boat in still water is 15 $\dfrac{km}{hr}$ and the velocity of the river stream is 10 $\dfrac{km}{hr}$. Find the time taken by the boat to travel 60 km downstream.
S olution:
Since the boat is travelling downstream, this means that the velocity of the boat and the river have the same direction.
We have been given:
v BW = 15$\dfrac{km}{hr}$, and v W = 10$\dfrac{km}{hr}$.
Using $v_{B W}=v_{B}-v_{W}$ we can find the value of v B .
v B = v BW + v W
v B = 15 + 10
v B = 25 \[ \dfrac{\mathrm{~km}}{ \mathrm{hr}} \]
The time taken by the boat to travel 60km will then be:
$\begin{align} &t=\dfrac{60}{v_{B}} \\ &t=\dfrac{60}{25} \\ &t=2.4 \mathrm{hr} \end{align}$
The velocity of an object in respect to another object is its relative velocity. It enables us to comprehend how objects move and interact with one another, relative velocity is crucial to understanding Physics. The velocity of an object with respect to another object is its relative velocity. It is a way to gauge how quickly two items are moving in relation to one another.
For a boat moving along a river or trying to cross a river, the concept of relative velocity is applied. Here, the velocity of the boat and the velocity of the water flow in the river flow are used to calculate the relative velocities. When a boat is moving across a river it moves at some particular angle with respect to the horizontal and evaluating these conditions can tell us the minimum time and the shortest path for the boat to cross the river.

FAQs on River Boat Problem in 2D From Relative Velocity - JEE Important Topic
1. What is the importance of the river boat problem in JEE Main?
River boat problem is a part of relative velocity. It is confusing at first, but is indeed an important topic for JEE Main . River boat problem is similar to other problems like rain man problems or the aeroplane problems. These problems are also solved using the techniques used in river boat problems. Every year at least 1 question is asked from the kinematics part and the probability of relative velocity being asked is quite high due to the variety of questions that can be framed.
2. What are absolute and relative velocities?
Relative velocity is the velocity calculated between objects in motion. It depends on the frame of reference of the objects and the observer. It changes with the choice of frame of reference. Absolute velocity on the other hand is the velocity that can be defined with respect to some absolute spatial coordinate system. This velocity will be independent of the frame of reference. We can only measure the relative velocity of any object with our present technology and knowledge about things.
- TPC and eLearning
- What's NEW at TPC?
- Read Watch Interact
- Practice Review Test
- Teacher-Tools
- Subscription Selection
- Seat Calculator
- Ad Free Account
- Edit Profile Settings
- Classes (Version 2)
- Student Progress Edit
- Task Properties
- Export Student Progress
- Task, Activities, and Scores
- Metric Conversions Questions
- Metric System Questions
- Metric Estimation Questions
- Significant Digits Questions
- Proportional Reasoning
- Acceleration
- Distance-Displacement
- Dots and Graphs
- Graph That Motion
- Match That Graph
- Name That Motion
- Motion Diagrams
- Pos'n Time Graphs Numerical
- Pos'n Time Graphs Conceptual
- Up And Down - Questions
- Balanced vs. Unbalanced Forces
- Change of State
- Force and Motion
- Mass and Weight
- Match That Free-Body Diagram
- Net Force (and Acceleration) Ranking Tasks
- Newton's Second Law
- Normal Force Card Sort
- Recognizing Forces
- Air Resistance and Skydiving
- Solve It! with Newton's Second Law
- Which One Doesn't Belong?
- Component Addition Questions
- Head-to-Tail Vector Addition
- Projectile Mathematics
- Trajectory - Angle Launched Projectiles
- Trajectory - Horizontally Launched Projectiles
- Vector Addition
- Vector Direction
- Which One Doesn't Belong? Projectile Motion
- Forces in 2-Dimensions
- Being Impulsive About Momentum
- Explosions - Law Breakers
- Hit and Stick Collisions - Law Breakers
- Case Studies: Impulse and Force
- Impulse-Momentum Change Table
- Keeping Track of Momentum - Hit and Stick
- Keeping Track of Momentum - Hit and Bounce
- What's Up (and Down) with KE and PE?
- Energy Conservation Questions
- Energy Dissipation Questions
- Energy Ranking Tasks
- LOL Charts (a.k.a., Energy Bar Charts)
- Match That Bar Chart
- Words and Charts Questions
- Name That Energy
- Stepping Up with PE and KE Questions
- Case Studies - Circular Motion
- Circular Logic
- Forces and Free-Body Diagrams in Circular Motion
- Gravitational Field Strength
- Universal Gravitation
- Angular Position and Displacement
- Linear and Angular Velocity
- Angular Acceleration
- Rotational Inertia
- Balanced vs. Unbalanced Torques
- Getting a Handle on Torque
- Torque-ing About Rotation
- Properties of Matter
- Fluid Pressure
- Buoyant Force
- Sinking, Floating, and Hanging
- Pascal's Principle
- Flow Velocity
- Bernoulli's Principle
- Balloon Interactions
- Charge and Charging
- Charge Interactions
- Charging by Induction
- Conductors and Insulators
- Coulombs Law
- Electric Field
- Electric Field Intensity
- Polarization
- Case Studies: Electric Power
- Know Your Potential
- Light Bulb Anatomy
- I = ∆V/R Equations as a Guide to Thinking
- Parallel Circuits - ∆V = I•R Calculations
- Resistance Ranking Tasks
- Series Circuits - ∆V = I•R Calculations
- Series vs. Parallel Circuits
- Equivalent Resistance
- Period and Frequency of a Pendulum
- Pendulum Motion: Velocity and Force
- Energy of a Pendulum
- Period and Frequency of a Mass on a Spring
- Horizontal Springs: Velocity and Force
- Vertical Springs: Velocity and Force
- Energy of a Mass on a Spring
- Decibel Scale
- Frequency and Period
- Closed-End Air Columns
- Name That Harmonic: Strings
- Rocking the Boat
- Wave Basics
- Matching Pairs: Wave Characteristics
- Wave Interference
- Waves - Case Studies
- Color Addition and Subtraction
- Color Filters
- If This, Then That: Color Subtraction
- Light Intensity
- Color Pigments
- Converging Lenses
- Curved Mirror Images
- Law of Reflection
- Refraction and Lenses
- Total Internal Reflection
- Who Can See Who?
- Formulas and Atom Counting
- Atomic Models
- Bond Polarity
- Entropy Questions
- Cell Voltage Questions
- Heat of Formation Questions
- Reduction Potential Questions
- Oxidation States Questions
- Measuring the Quantity of Heat
- Hess's Law
- Oxidation-Reduction Questions
- Galvanic Cells Questions
- Thermal Stoichiometry
- Molecular Polarity
- Quantum Mechanics
- Balancing Chemical Equations
- Bronsted-Lowry Model of Acids and Bases
- Classification of Matter
- Collision Model of Reaction Rates
- Density Ranking Tasks
- Dissociation Reactions
- Complete Electron Configurations
- Elemental Measures
- Enthalpy Change Questions
- Equilibrium Concept
- Equilibrium Constant Expression
- Equilibrium Calculations - Questions
- Equilibrium ICE Table
- Intermolecular Forces Questions
- Ionic Bonding
- Lewis Electron Dot Structures
- Limiting Reactants
- Line Spectra Questions
- Mass Stoichiometry
- Measurement and Numbers
- Metals, Nonmetals, and Metalloids
- Metric Estimations
- Metric System
- Molarity Ranking Tasks
- Mole Conversions
- Name That Element
- Names to Formulas
- Names to Formulas 2
- Nuclear Decay
- Particles, Words, and Formulas
- Periodic Trends
- Precipitation Reactions and Net Ionic Equations
- Pressure Concepts
- Pressure-Temperature Gas Law
- Pressure-Volume Gas Law
- Chemical Reaction Types
- Significant Digits and Measurement
- States Of Matter Exercise
- Stoichiometry Law Breakers
- Stoichiometry - Math Relationships
- Subatomic Particles
- Spontaneity and Driving Forces
- Gibbs Free Energy
- Volume-Temperature Gas Law
- Acid-Base Properties
- Energy and Chemical Reactions
- Chemical and Physical Properties
- Valence Shell Electron Pair Repulsion Theory
- Writing Balanced Chemical Equations
- Mission CG1
- Mission CG10
- Mission CG2
- Mission CG3
- Mission CG4
- Mission CG5
- Mission CG6
- Mission CG7
- Mission CG8
- Mission CG9
- Mission EC1
- Mission EC10
- Mission EC11
- Mission EC12
- Mission EC2
- Mission EC3
- Mission EC4
- Mission EC5
- Mission EC6
- Mission EC7
- Mission EC8
- Mission EC9
- Mission RL1
- Mission RL2
- Mission RL3
- Mission RL4
- Mission RL5
- Mission RL6
- Mission KG7
- Mission RL8
- Mission KG9
- Mission RL10
- Mission RL11
- Mission RM1
- Mission RM2
- Mission RM3
- Mission RM4
- Mission RM5
- Mission RM6
- Mission RM8
- Mission RM10
- Mission LC1
- Mission RM11
- Mission LC2
- Mission LC3
- Mission LC4
- Mission LC5
- Mission LC6
- Mission LC8
- Mission SM1
- Mission SM2
- Mission SM3
- Mission SM4
- Mission SM5
- Mission SM6
- Mission SM8
- Mission SM10
- Mission KG10
- Mission SM11
- Mission KG2
- Mission KG3
- Mission KG4
- Mission KG5
- Mission KG6
- Mission KG8
- Mission KG11
- Mission F2D1
- Mission F2D2
- Mission F2D3
- Mission F2D4
- Mission F2D5
- Mission F2D6
- Mission KC1
- Mission KC2
- Mission KC3
- Mission KC4
- Mission KC5
- Mission KC6
- Mission KC7
- Mission KC8
- Mission AAA
- Mission SM9
- Mission LC7
- Mission LC9
- Mission NL1
- Mission NL2
- Mission NL3
- Mission NL4
- Mission NL5
- Mission NL6
- Mission NL7
- Mission NL8
- Mission NL9
- Mission NL10
- Mission NL11
- Mission NL12
- Mission MC1
- Mission MC10
- Mission MC2
- Mission MC3
- Mission MC4
- Mission MC5
- Mission MC6
- Mission MC7
- Mission MC8
- Mission MC9
- Mission RM7
- Mission RM9
- Mission RL7
- Mission RL9
- Mission SM7
- Mission SE1
- Mission SE10
- Mission SE11
- Mission SE12
- Mission SE2
- Mission SE3
- Mission SE4
- Mission SE5
- Mission SE6
- Mission SE7
- Mission SE8
- Mission SE9
- Mission VP1
- Mission VP10
- Mission VP2
- Mission VP3
- Mission VP4
- Mission VP5
- Mission VP6
- Mission VP7
- Mission VP8
- Mission VP9
- Mission WM1
- Mission WM2
- Mission WM3
- Mission WM4
- Mission WM5
- Mission WM6
- Mission WM7
- Mission WM8
- Mission WE1
- Mission WE10
- Mission WE2
- Mission WE3
- Mission WE4
- Mission WE5
- Mission WE6
- Mission WE7
- Mission WE8
- Mission WE9
- Vector Walk Interactive
- Name That Motion Interactive
- Kinematic Graphing 1 Concept Checker
- Kinematic Graphing 2 Concept Checker
- Graph That Motion Interactive
- Two Stage Rocket Interactive
- Rocket Sled Concept Checker
- Force Concept Checker
- Free-Body Diagrams Concept Checker
- Free-Body Diagrams The Sequel Concept Checker
- Skydiving Concept Checker
- Elevator Ride Concept Checker
- Vector Addition Concept Checker
- Vector Walk in Two Dimensions Interactive
- Name That Vector Interactive
- River Boat Simulator Concept Checker
- Projectile Simulator 2 Concept Checker
- Projectile Simulator 3 Concept Checker
- Hit the Target Interactive
- Turd the Target 1 Interactive
- Turd the Target 2 Interactive
- Balance It Interactive
- Go For The Gold Interactive
- Egg Drop Concept Checker
- Fish Catch Concept Checker
- Exploding Carts Concept Checker
- Collision Carts - Inelastic Collisions Concept Checker
- Its All Uphill Concept Checker
- Stopping Distance Concept Checker
- Chart That Motion Interactive
- Roller Coaster Model Concept Checker
- Uniform Circular Motion Concept Checker
- Horizontal Circle Simulation Concept Checker
- Vertical Circle Simulation Concept Checker
- Race Track Concept Checker
- Gravitational Fields Concept Checker
- Orbital Motion Concept Checker
- Angular Acceleration Concept Checker
- Balance Beam Concept Checker
- Torque Balancer Concept Checker
- Aluminum Can Polarization Concept Checker
- Charging Concept Checker
- Name That Charge Simulation
- Coulomb's Law Concept Checker
- Electric Field Lines Concept Checker
- Put the Charge in the Goal Concept Checker
- Circuit Builder Concept Checker (Series Circuits)
- Circuit Builder Concept Checker (Parallel Circuits)
- Circuit Builder Concept Checker (∆V-I-R)
- Circuit Builder Concept Checker (Voltage Drop)
- Equivalent Resistance Interactive
- Pendulum Motion Simulation Concept Checker
- Mass on a Spring Simulation Concept Checker
- Particle Wave Simulation Concept Checker
- Boundary Behavior Simulation Concept Checker
- Slinky Wave Simulator Concept Checker
- Simple Wave Simulator Concept Checker
- Wave Addition Simulation Concept Checker
- Standing Wave Maker Simulation Concept Checker
- Color Addition Concept Checker
- Painting With CMY Concept Checker
- Stage Lighting Concept Checker
- Filtering Away Concept Checker
- InterferencePatterns Concept Checker
- Young's Experiment Interactive
- Plane Mirror Images Interactive
- Who Can See Who Concept Checker
- Optics Bench (Mirrors) Concept Checker
- Name That Image (Mirrors) Interactive
- Refraction Concept Checker
- Total Internal Reflection Concept Checker
- Optics Bench (Lenses) Concept Checker
- Kinematics Preview
- Velocity Time Graphs Preview
- Moving Cart on an Inclined Plane Preview
- Stopping Distance Preview
- Cart, Bricks, and Bands Preview
- Fan Cart Study Preview
- Friction Preview
- Coffee Filter Lab Preview
- Friction, Speed, and Stopping Distance Preview
- Up and Down Preview
- Projectile Range Preview
- Ballistics Preview
- Juggling Preview
- Marshmallow Launcher Preview
- Air Bag Safety Preview
- Colliding Carts Preview
- Collisions Preview
- Engineering Safer Helmets Preview
- Push the Plow Preview
- Its All Uphill Preview
- Energy on an Incline Preview
- Modeling Roller Coasters Preview
- Hot Wheels Stopping Distance Preview
- Ball Bat Collision Preview
- Energy in Fields Preview
- Weightlessness Training Preview
- Roller Coaster Loops Preview
- Universal Gravitation Preview
- Keplers Laws Preview
- Kepler's Third Law Preview
- Charge Interactions Preview
- Sticky Tape Experiments Preview
- Wire Gauge Preview
- Voltage, Current, and Resistance Preview
- Light Bulb Resistance Preview
- Series and Parallel Circuits Preview
- Thermal Equilibrium Preview
- Linear Expansion Preview
- Heating Curves Preview
- Electricity and Magnetism - Part 1 Preview
- Electricity and Magnetism - Part 2 Preview
- Vibrating Mass on a Spring Preview
- Period of a Pendulum Preview
- Wave Speed Preview
- Slinky-Experiments Preview
- Standing Waves in a Rope Preview
- Sound as a Pressure Wave Preview
- DeciBel Scale Preview
- DeciBels, Phons, and Sones Preview
- Sound of Music Preview
- Shedding Light on Light Bulbs Preview
- Models of Light Preview
- Electromagnetic Radiation Preview
- Electromagnetic Spectrum Preview
- EM Wave Communication Preview
- Digitized Data Preview
- Light Intensity Preview
- Concave Mirrors Preview
- Object Image Relations Preview
- Snells Law Preview
- Reflection vs. Transmission Preview
- Magnification Lab Preview
- Reactivity Preview
- Ions and the Periodic Table Preview
- Periodic Trends Preview
- Intermolecular Forces Preview
- Melting Points and Boiling Points Preview
- Reaction Rates Preview
- Ammonia Factory Preview
- Stoichiometry Preview
- Nuclear Chemistry Preview
- Gaining Teacher Access
- Tasks and Classes
- Tasks - Classic
- Subscription
- Subscription Locator
- 1-D Kinematics
- Newton's Laws
- Vectors - Motion and Forces in Two Dimensions
- Momentum and Its Conservation
- Work and Energy
- Circular Motion and Satellite Motion
- Thermal Physics
- Static Electricity
- Electric Circuits
- Vibrations and Waves
- Sound Waves and Music
- Light and Color
- Reflection and Mirrors
- About the Physics Interactives
- Task Tracker
- Usage Policy
- Newtons Laws
- Vectors and Projectiles
- Forces in 2D
- Momentum and Collisions
- Circular and Satellite Motion
- Balance and Rotation
- Electromagnetism
- Waves and Sound
- Atomic Physics
- Forces in Two Dimensions
- Work, Energy, and Power
- Circular Motion and Gravitation
- Sound Waves
- 1-Dimensional Kinematics
- Circular, Satellite, and Rotational Motion
- Einstein's Theory of Special Relativity
- Waves, Sound and Light
- QuickTime Movies
- About the Concept Builders
- Pricing For Schools
- Directions for Version 2
- Measurement and Units
- Relationships and Graphs
- Rotation and Balance
- Vibrational Motion
- Reflection and Refraction
- Teacher Accounts
- Task Tracker Directions
- Kinematic Concepts
- Kinematic Graphing
- Wave Motion
- Sound and Music
- About CalcPad
- 1D Kinematics
- Vectors and Forces in 2D
- Simple Harmonic Motion
- Rotational Kinematics
- Rotation and Torque
- Rotational Dynamics
- Electric Fields, Potential, and Capacitance
- Transient RC Circuits
- Light Waves
- Units and Measurement
- Stoichiometry
- Molarity and Solutions
- Thermal Chemistry
- Acids and Bases
- Kinetics and Equilibrium
- Solution Equilibria
- Oxidation-Reduction
- Nuclear Chemistry
- Newton's Laws of Motion
- Work and Energy Packet
- Static Electricity Review
- NGSS Alignments
- 1D-Kinematics
- Projectiles
- Circular Motion
- Magnetism and Electromagnetism
- Graphing Practice
- About the ACT
- ACT Preparation
- For Teachers
- Other Resources
- Solutions Guide
- Solutions Guide Digital Download
- Motion in One Dimension
- Work, Energy and Power
- Algebra Based Physics
- Other Tools
- Frequently Asked Questions
- Purchasing the Download
- Purchasing the CD
- Purchasing the Digital Download
- About the NGSS Corner
- NGSS Search
- Force and Motion DCIs - High School
- Energy DCIs - High School
- Wave Applications DCIs - High School
- Force and Motion PEs - High School
- Energy PEs - High School
- Wave Applications PEs - High School
- Crosscutting Concepts
- The Practices
- Physics Topics
- NGSS Corner: Activity List
- NGSS Corner: Infographics
- About the Toolkits
- Position-Velocity-Acceleration
- Position-Time Graphs
- Velocity-Time Graphs
- Newton's First Law
- Newton's Second Law
- Newton's Third Law
- Terminal Velocity
- Projectile Motion
- Forces in 2 Dimensions
- Impulse and Momentum Change
- Momentum Conservation
- Work-Energy Fundamentals
- Work-Energy Relationship
- Roller Coaster Physics
- Satellite Motion
- Electric Fields
- Circuit Concepts
- Series Circuits
- Parallel Circuits
- Describing-Waves
- Wave Behavior Toolkit
- Standing Wave Patterns
- Resonating Air Columns
- Wave Model of Light
- Plane Mirrors
- Curved Mirrors
- Teacher Guide
- Using Lab Notebooks
- Current Electricity
- Light Waves and Color
- Reflection and Ray Model of Light
- Refraction and Ray Model of Light
- Classes (Legacy Version)
- Teacher Resources
- Subscriptions

- Newton's Laws
- Einstein's Theory of Special Relativity
- About Concept Checkers
- School Pricing
- Newton's Laws of Motion
- Newton's First Law
- Newton's Third Law
elative Velocity and River Boat Problems Video Tutorial
The Relative Velocity and River Boat Problems Video Tutorial discusses the concept of relative velocity. The concept is applied to explain the analysis of the motion of planes moving amidst winds and the motion of boats heading up, down, and across a river in the presence of a current. The video lesson answers the following questions:
- What is meant by the term relative velocity?
- When a boat heads up, down or across a river, what effect does the river current have on the boat’s motion?
View on YouTube

COMMENTS
In our problem, the 80 m corresponds to the distance A, and so the average speed of 4 m/s (average speed in the direction straight across the river) should be substituted into the equation to determine the time. time = (80 m)/ (4 m/s) = 20 s. It requires 20 s for the boat to travel across the river.
See answer Problem # 3 A duck swims at a constant speed from one side of a river to the other side in a time of 4 seconds. The river is 6 meters wide and it is flowing at a speed of 2 m/s. ... See answer Answers For Relative Velocity Problems Answer for Problem # 2 You first have to assume that the truck velocity and relative ball velocity are ...
If the PDF does not show in the window above, then you can access it directly here: Relative Velocity and Riverboat Problems (PDF) The Curriculum Corner contains a complete ready-to-use curriculum for the high school physics classroom. This collection of pages comprise worksheets in PDF format that developmentally target key concepts and ...
Relative Velocity Problems. Problem (1): A person walks across a raft at a speed of 0.5\,\rm m/s 0.5m/s while his raft is traveling down the river at a speed of 1.8\,\rm m/s 1.8m/s relative to the riverbank. Assuming that he walks perpendicular to the raft's motion relative to the river current, what is the person's velocity with respect to the ...
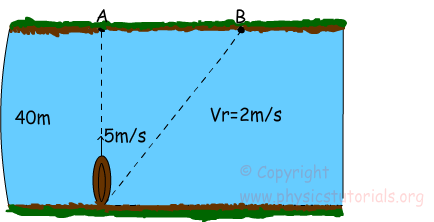
Riverboat Problems. Example: Boat has velocity 5m/s with respect to the river. It aims to reach point A, however, because of the river speed it reaches another point B. If the speed of current is 2m/s to the east calculate the time of trip and the distance between A and B. Boat follows the path shown in dashed line which is the direction of the resultant vector.
a. Determine the resultant velocity of the riverboat (velocity with respect to the shore). b. If the river is 71.0 m wide, then determine the time required for the boat to cross the river. c. Determine the distance that the boat will travel downstream. 5. Suppose that the boat attempts this same task of crossing the river (5.1 m/s with respect ...
Relative Motion - Riverboat problem. A river has a width d = 40 m. The water flows at a constant velocity vA = - 6 i (m/s) with respect to a frame of reference at rest O . A boat wants to cross the river from point A on one bank to point B on the other (see figure). The velocity vector of the boat with respect to the water is: v'B = 4 j (m/s).
a. Determine the resultant velocity of the riverboat (velocity with respect to the shore). b. If the river is 71.0 m wide, then determine the time required for the boat to cross the river. c. Determine the distance that the boat will travel downstream. 5. Suppose that the boat attempts this same task of crossing the river (5.1 m/s with respect ...
We need to draw the vector component diagram for →VBG to determine the direction and magnitude of the velocity of the boat relative to the ground. We then use the Pythagorean Theorem to get the magnitude of the velocity of the boat relative to the ground, →VBG = √V2BGx + V2BGy. →VBG = √(11.299m / s)2 + (10.82m / s)2.
The velocity of the plane = V a = 100 km/hr. The relative velocity of the plane with respect to the ground can be given as. The angle between the velocity of the wind and that of the plane is 90°. Using the Pythagorean theorem, the resultant velocity can be calculated as, R 2 = (100 km/hr) 2 + (25 km/hr) 2. R 2 = 10 000 km 2 /hr 2 + 625 km 2 ...
Before proceeding to the next step, lets determine "the velocity of the water relative to the freighter", V. wf. The following is a unique feature of case 2 relative velocity problems. That is V. wf. = - Vfw. This means the size of both velocities are the same, but the directions of each are perfectly opposing.
Physics Ninja looks at 2 problems involving a boat crossing a river. In Problem 1 we find the distance traveled downstream and in problem 2 we find the ang...
Unit 2: 2D-Kinematics & Relative Velocity Practice Problems. Note: problem difficulty is ranked using a star system. ... If the river was 12m wide and flowing straight North at 3m/s, what must have been your velocity relative to the water? ***Q2.8) A plane wants to fly from Toronto to guelph in 30 minutes. If the city of Guelph is located 60km ...
oPhysics. Description. This is a simulation of a boat crossing a river. Adjust the direction the boat is aimed, the boat's velocity relative to the river, and the river's velocity relative to the earth. Press the "Run" button to watch the boat's trip across the river. Questions to answer: 1) What direction should the boat be aimed to get to the ...
Numerical Examples of Relative Velocity River Boat Problems. Example 1: A boat has a velocity of 10$\dfrac {km} {hr}$ in still water and it crosses a river of width 2 km. If the boat crosses the river along the shortest path possible in 30 minutes, calculate the velocity of the river water. Solution:
Problem 1: Across the river that flows with a rate of 4 m/s, Mr. Pepper swims at the velocity of 3 m/s. Find his velocity relative to the Earth. Solution: We are given three reference frames: the river (R), Mr. Pepper (M), and the Earth (E). We know that the velocity of the river relative to the Earth V R/E-X = 4 m/s while
Unformatted text preview: Vectors and Projectiles Name: \ m l Relative Velocity and Riverboat Problems Read from Lesson 1 of the Vectors and Motion in Two-Dimensions chapter at The Physics Classroom: MOP Connection: Vectors and Projectiles: sublevel 6 (and maybe sublevel 5) 1. Planes fly in a medium of moving air (winds), providing an example of relative motion.
The Relative Velocity and River Boat Problems Video Tutorial discusses the concept of relative velocity. The concept is applied to explain the analysis of the motion of planes moving amidst winds and the motion of boats heading up, down, and across a river in the presence of a current. The video lesson answers the following questions:
Relative Velocity and River Boat Problems Lesson Notes Relative Velocity On occasion, an object will move within a medium that is moving with respect to an observer. On such occasions, an observer on the moving object will observe a different speed as an observer on a "stationary" reference frame. We would say that the velocity of the ...
Relative Velocity and Riverboat Problems Answers only.pdf -. Doc Preview. Pages 2. Total views 46. West Forsyth High School. SCIENCE. SCIENCE NOT SURE. CorporalSwan344. 10/4/2020.
The Relative Velocity and River Boat Problems Video Tutorial discusses the concept of relative velocity. The concept is applied to explain the analysis of the motion of planes moving amidst winds and the motion of boats heading up, down, and across a river in the presence of a current. The video lesson answers the following questions: